Dott. Ing. Flavio Mattavelli
Calcolando
il Punto Neutro = PN, o NP (Neutral
Point), con le conseguenti posizioni del Centro
di Gravità = CG, solo nel caso di un aeromodello convenzionale.
Prefazione.
PN qui è sempre riferito all’intero velivolo, ma i metodi
pratici sono accettabili solo nei casi di aeromodelli ed uccelli, mentre per
aerei è indispensabile calcolare la posizione del PN con metodi più validi,
solitamente inattuabili in pratica dagli aeromodellisti (me compreso).
Per il significato di PN distinto dal
CA, dal CP e dal C (centri rispettivamente = centro aerodinamico dell’ala,
centro di pressione dell’ala, punto di controllo stabilizzatore) vedere il mio articolo Fuochi…
Aeromodello convenzionale significa con ala anteriore ed impennaggi in coda,
cioè volante quasi come negli uccelli.
E’ sottinteso che i comandi s’intendono bloccati a zero
quando il piano orizzontale di coda (o stabilatore),
insieme dello stabilizzatore fisso e della parte mobile (o elevatore, o
equilibratore, o spatolino che dir si voglia), è fisso nella posizione
centrale, con flaps e quant’altro tutti a zero inclinazioni, rispetto al
progetto idealmente operativo, cioè senza modificare il diedro longitudinale geometrico (= DL, cioè
l’angolazione geometrica tra ala e stabilatore).
Tale diedro di solito è compreso tra
0° e < 8°, ma talora si può mutare in fase costruttiva prima del volo, che
poi sarà a comandi liberi.
Notare che esiste un diedro
longitudinale geometrico, che è quello che si può misurare, ed un diedro longitudinale assoluto o aerodinamico, angolo tra i
piani di portanza zero, che è quello che determina realmente il PN del
velivolo, ma non si può misurare. Quello assoluto supera il geometrico di qualche
grado e/o frazione di grado.
La posizione del CG può variare
accettabilmente entro un campo determinato dal DL, cioè esistono diversi
diedri longitudinali validi per diversi CG, tuttavia non c’è una regola unica,
calcolabile esattamente; comunque, a parte aver fissato il DL con incidenza ala
maggiore dell’incidenza della coda posteriore, l’entità del DL determina la
posizione del PN e quindi quella del CG.
Si dovrebbe
regolare il CG ottimale dopo prove sperimentali con un certo DL, ma c’è anche
chi regola il DL dopo aver prefissato il CG che più gli aggrada.
In generale un DL
maggiore richiede spostare il PN ed il CG in avanti e viceversa.
Cambiare il DL ad
equilibratore bloccato equivale qualitativamente a sbloccare i comandi
longitudinali a DL costante, però quantitativamente gli effetti dinamici
possono essere diversi (vedere il topic Habitch nel forum Barone Rosso, colà
dopo la pagina 6). Si è molto discusso nel forum Barone Rosso sul diedro longitudinale
(ad esempio), però senza formule definitive.
In quest’articolo
intendo sempre il DL “trimmato”a
comandi bloccati, per il tipo di volo preferito. La cosa vale soprattutto per
il tipo di planata degli alianti, vedere poco avanti, riguardo alle velocità di
planata.
Alla fine di
quest’articolo proporrò una semplice
formula contenente il DL geometrico, formula che, pur essendo molto
empirica ed approssimativa, per me è meglio di niente, siccome di solito ci si
appoggia esclusivamente alla pratica, quasi senza teoria. Ci sono 3 vie per
arrivare ad un CG ottimale: tanta esperienza pratica e poca teoria di base,
tanta teoria e poca pratica, oppure nessuna teoria, nessuna pratica e tanta
fortuna.
Molti
aeromodellisti sono convinti che mettere il CG sempre "standard"
quasi al 30%, max. 35%, circa della MAC (Mean Aerodynamic Chord = corda aerodinamica media, v. avanti),
proiettandone poi la posizione sull'asse longitudinale, cioè sulla fusoliera di
un aeromodello convenzionale, sia la soluzione ideale. E’ certamente la
soluzione più facile, probabilmente il modello volerà quasi sempre, ma c'è
differenza tra volare e volare bene.
Se sostenete la teoria del CG quasi 30% potete tralasciare di leggere
il resto dell’articolo.
Altri credono che
invece basti fidarsi dei numerosi moderni calcolatori on line editabili, che
offrono direttamente la posizione del CG dopo l’introduzione di pochi dati
reperibili dalla geometria del modello. Penso che tali calcolatori siano utili
per trovare la MAC, ma siano imprecisi, cioè solo approssimativi, per la
posizione del CG.
Esistono infatti diversi calcolatori
on line (spesso in inglese), dal più rozzo al più sofisticato, ma in realtà
sono tutti solo orientativi, aventi per scopo di trovare la MAC e soprattutto
una posizione approssimativa del CG sulla MAC.
L’acronimo MAC senza altre indicazioni è riferito soltanto all’ala, ma ovviamente potrebbe essere
riferibile anche ad ogni superficie aerodinamica (esiste ad esempio anche la
MAC del piano orizzontale).
La MAC alare può venir calcolata
tramite i medesimi calcolatori editabili on line, o tramite file excel; nei casi più semplici di ali trapezoidali io
preferisco l’usuale metodo grafico
(per ali trapezoidali vedere avanti nel riquadro giallino). Il concetto di MAC
può venir erroneamente confuso con la media geometrica delle corde,
praticamente è quasi lo stesso, dunque non insisterò sulle differenze.
Qui approfondirò solo come calcolare
il punto neutro in percentuali della MAC, però tralasciando lo storico metodo
di Crocco per trovare il campo dei CG utili.
Trovata infatti la MAC, i calcolatori
più semplici si limitano a consigliare di porre
il CG, nel senso di marcia, dietro al 25% a partire dal bordo di entrata
(25% che sarebbe la posizione della maggioranza dei centri aerodinamici dell’ala), aggiungendo + 5~10%, senza precisare la posizione del
punto neutro del velivolo, che dovrebbe essere ancora più arretrata.
Ciò vale solo per aerei convenzionali, mentre
per i tuttala ed i canard il CG va posto davanti al 25%, nel senso di marcia
(ma qui non tratterò canard e tuttala).
Notare che, mentre il PN ha un’unica
posizione di equilibrio a comandi bloccati, il CG potrebbe assumere diverse posizioni staticamente stabili, ma dal diverso
comportamento dinamico, entro una gamma accettabile di posizioni, ognuna
più adatta per il tipo di volo desiderato, con diversi DL.
Una volta trovato il PN può sembrare
(erroneamente) una bazzecola porgli davanti il CG tramite la distanza
denominata margine statico;
normalmente esso è una lunghezza tra il
5 ed il 15 % della MAC alare, tuttavia il vero problema è trovare l’esatta
posizione del PN; inoltre occorre tener presente che il margine statico, sempre
maggiore di zero, non deve nemmeno divenire eccessivo, direi mai oltre il 20%,
valore per il quale il modello sarebbe in pratica sempre picchiato.
Attenzione che si può fare un margine statico alto (o basso) con grande diedro
longitudinale e un margine statico
basso (o alto) con piccolo diedro longitudinale, intendendo sempre il DL a
comandi bloccati.
In caso di planata uniforme senza
motore cambierà la velocità di caduta libera, come ben spiegato in Manuale di
volo libero:
·
Velocità di trim. Un velivolo ben equilibrato, quando lasciato libero di planare in
modo stabilizzato (in aria calma) senza che gli vengano impartiti comandi,
volerà con un angolo di incidenza determinato dalle sue caratteristiche
strutturali e di regolazione: esso scenderà, pertanto, secondo un piano
inclinato costante, ad una velocità altrettanto costante; tale velocità, che
varia da apparecchio ad apparecchio, è detta velocità di trim (o
di regolazione).
·
Velocità di minima caduta. Aumentando
l'angolo di incidenza, l'ala rallenta, fino a raggiungere la velocità
di minima caduta: in aria calma e a parità di quota questa velocità è
quella che ci permette di stare in aria più a lungo. Per aumentare
l’incidenza si può azionare in volo l’elevatore, ma anche si poteva aumentare
il DL prima del volo, con aumento di resistenza, nei così detti modelli “galleggioni”. Che la velocità di caduta sia minima non
significa che avvenga alla massima efficienza, anzi la pendenza di planata, in
un tempo doppio, potrebbe dimezzarsi.
·
Velocità di stallo. Aumentando
ulteriormente l'angolo di incidenza, si supera quello critico di stallo (si può
dire che la velocità è scesa al di sotto della velocità di stallo)
e l'apparecchio non vola più.
·
Velocità di massima efficienza. Se
invece, partendo sempre dalla velocità di trim, riduciamo l'angolo di
incidenza, l'apparecchio accelera, fino a raggiungere la velocità di
massima efficienza: è questa la velocità alla quale diviene ottimale il
rapporto tra caduta ed avanzamento, in altri termini, in aria calma, è la
velocità che ci permette di andare più lontano.
·
Velocità massima. Picchiando
ulteriormente (riducendo ancora di più l'incidenza) la traiettoria diviene
molto ripida, e si viaggia alla velocità massima raggiungibile in
sicurezza.
Il diedro longitudinale assoluto (o l’elevatore sempre
in basso) non deve essere sempre negativo, altrimenti il volo si tramuta in
looping inverso.
Al limite si potrebbe fare diedro
long. assoluto zero e CG con margine statico zero rispetto all’esatto PN,
l’equilibrio sarebbe con stabilità indifferente, ingovernabile da un pilota
umano.
Il PN potrebbe arretrare anche dietro la MAC, ma il CG deve sempre stare
davanti al PN, nel
senso di marcia. Se il CG arretrasse dietro al PN il peso farebbe scampanare
malamente il velivolo.
Infine non occorrerebbe tralasciare
il così detto centraggio dinamico tramite la “prova
dell’affondata”, che però io qui ho tralasciato.
Inizio dei calcoli del PN.
Nei calcolatori on line più grezzi il
PN viene supposto considerando approssimativamente un CG al 30% MAC ed il
margine statico perlopiù al 10 %, ma le posizioni minima e massima dei
possibili CG, nonché quella esatta del PN restano ambigue; per i convenzionali ad esempio il PN viene talvolta
indicato al 25% + 5~10% + 10% = 40~45 % dal bordo d’entrata della MAC, il che talvolta può essere giusto, ma
spesso non è esatto, ad esempio negli aeromodelli Old
timer il PN era spesso dietro al bordo di uscita della MAC.
Gli esempi vengono evidenziati in viola. Il suddetto CG è stato
indicato al 30~35% MAC a partire dal bordo di entrata, però, se il PN
fosse al 42,5%, il CG potrebbe venir meglio consigliato da circa il 27,5% fino
al 37,5%, incentrato sul 32,5%, pur potendosi tollerare un CG circa anche dal
22,5% (con modello picchiato qualora < 22,5%) al 42,5%, mentre con il CG
oltre il 42,5% il modello sarebbe instabile (ultra cabrato), ma ciò non è vero
per alcuni modelli Old timer.
Simbologia.
S’intenda che tutta questa
trattazione vale solo per I convenzionali. Molti simboli derivano da testi
inglesi. Chiedo scusa se mi capiterà di alternare alcuni simboli diversi, ma
con lo stesso significato, tipico caso di sinonimia (sono fin troppo abituato
ai sinonimi studiando le conchiglie delle marginelle,
in un’altra Sezione del mio presente sito Web).
K = Vbar = Vh = (Horizontal) Tail Volume
Ratio = HTVR = HTVC (C = coefficient) = HTPC (P
= plan) = rapporto volumetrico di coda (orizzontale), che per definizione significa:
K = (Tail
area/Wing area)*(L/Wing MAC) = (Area stabilatore*L) /
(Area ala*MAC ala)
Fare
attenzione che in qualche testo antico per K si intende l’inverso del presente
K.
AC = CA
= centro aerodinamico, a partire dal bordo di entrata, ritenuto sempre = 0,25
MAC = 25% MAC
Sia per
ala che stabilatore s’intendano entrambi i CA posti
al 25% della loro MAC, sebbene ciò non sia sempre esatto.
L = tail arm = braccio di coda, o
distanza tra il centro aerodinamico dell’ala e quello dello stabilatore
(normalmente L = da 2 a < 5 volte la lunghezza MAC).
DL =
diedro longitudinale geometrico in gradi sessagesimali
NP = neutral point = PN = punto
neutro, posizione % a partire dal bordo di entrata della MAC
CG =
posizione percentuale del centro di gravità a partire dal bordo di entrata
della MAC
AR
= aspect ratio = allungamento, talora
distinto in ARw = ARa
= allungamento dell’ala (wing) e distinto in ARc = ARt = allungamento del
piano orizzontale di coda (tail).
Wing MAC
= corda media aerodinamica dell’ala, indicata perlopiù solo MAC
D =
distanza incognita tra il centro aerodinamico dell’ala ed il punto neutro, oggetto principale del presente studio
Sa =
superficie alare = wing area
Sc = sup. del piano orizz. di coda (cioè stabilizzatore fisso + l’elevatore mobile
bloccato = stabilatore) = Tail
area = Stab.area
Φ
= ϕ = numero aureo, vedere capitolo Aerodinamica mirabolante (*).
Nota per timoni a V.
Nel
caso di timoni a V la superficie di coda da considerare in K, ai fini della
stabilità longitudinale, non è quella realmente misurabile, non è nemmeno la
sua proiezione sul piano orizzontale, bensì sarebbe quella risultante da Sc
*cos^2 (δ), dove δ è l’angolo tra la semi superficie del piano di
coda ed il piano orizzontale (secondo Drela).
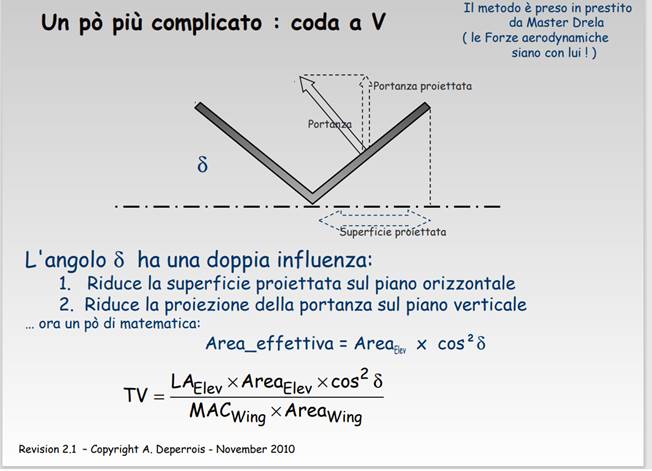
Ecco un’immagine
copiata dall’Analisi di XFLR5, pag. 14 (dove TV = K, LAElev = L ed Elev
= stabilatore a V):
Esempio
per timoni a V = 110 °, δ = 35°, cos 35° = 0,819, cos^2(δ) = 0,670.
Ritenendo le
portanze proporzionali alle superfici generanti, nei timoni a V, la portanza
utile per la stabilità longitudinale potrebbe essere la somma delle 2
componenti verticali della vera forza ortogonale alla coda (forza che è
inclinata in 2 semi forze dirette verso l’interno della V). Tali 2 componenti
lavorano insieme e sono proporzionali a Sc *cos (δ), ove Sc è la
superficie reale della coda a V = Area Elev.
La superficie di
coda proiettata sul piano orizzontale è una superficie minore di Sc,
precisamente è ancora Sc *cos (δ), ma è solo un’area virtuale che non è la
responsabile di tali componenti, che invece dipendono da quanto Sc è inclinata
sull’orizzontale, cioè dal diedro δ.
Man mano che
aumenta δ diminuiscono le 2 componenti.
Possiamo vedere che
l’area efficace di Sc ai fini della stabilità longitudinale è solo quella
riproiettata su Sc dalla proiezione orizzontale precedente, cioè Sc * cos
(δ) * cos (δ).
Questo passaggio
non mi è chiaro e lo ripeto nel seguito (ma purtroppo per me resta ancora
oscuro).
La reazione al
beccheggio non dipende da tutta la sup. della V, ma
solo da una parte dell’area spazzata nel beccheggio, che è la proiezione di Sc
sul piano orizzontale, cioè Sc * cos δ, proiezione che però è una
superficie solo virtuale, che reagisce realmente solo quando sostituita dalla
Sc reale, che ha le componenti verticali della portanza ridotte dal cos δ,
dunque la superficie effettivamente reagente è Sc * cos2 δ.
La variazione della
forza di coda che riguarda la stabilità dinamica longitudinale, vista come
variazione delle 2 componenti verticali effettivamente portanti, comporta inoltre
dover considerare Sc *cos^2 (δ) anche nel K = TV dei timoni a V, che va riferito sempre alla superficie del
timone orizzontale efficace equivalente.
In passato si
considerava erroneamente solo il coseno semplice, come “regola della nonna”, con
tutto il rispetto per le nonne, trascurando che esiste invece effettivamente
una maggior riduzione di superficie efficace longitudinalmente, in dipendenza
da cos2 δ, rispetto alla semplice proiezione orizzontale.
Analogamente esiste
una maggior riduzione di superficie efficace direzionalmente,
in dipendenza da sen2 δ, per quanto riguarda la stabilità
direzionale delle code a V, rispetto alle proiez. verticali, però le componenti orizzontali di deriva
raddoppiano e talora è un vantaggio.
Esplicitazione. In pratica si preferisce considerare
la lunghezza D come una percentuale della lunghezza MAC. Dividendo le lunghezze
D/MAC si ottiene la % di MAC corrispondente a D, scritta D%. Esempio
D% = 10% significa che D = 0,1 MAC = MAC * 10/100
Lunghezza
D = (D/MAC) * MAC.
Le
modalità di scrittura delle % possono indurre in confusione, spero di non
accrescerla, perché potrei scrivere 0,1 = 10% dimenticando, ma sottintendendo
sempre il riferimento alla MAC.
Bilanciamento grossolano delle superfici.
Sappiamo
che Sc può variare di solito da 1/4 ad 1/12 di Sa. Poniamoci il problema di trovare quel punto
intermedio (PN) da bilanciare le sole portanze generabili dalle superfici in
volo supposto statico, con le portanze proporzionali alle superfici, portanze
supposte applicate nei rispettivi CA (in realtà le portanze non dipendono solo
dalle S, ma il calcolo con le sole S è immediato).
Facciamo 2 esempi, senza fossilizzarsi sulle unità di
misura diverse, uguagliando i momenti delle portanze
rispetto al PN incognito, trascurando le masse (per ora).
Istituiamo
pertanto la (errata) relazione intuitiva Sa * D =
(L-D) * Sc
1) Sa
= 60, Sc = 15, L = 400, MAC = 100, D = x
60*x
= (L-x) *15, donde si ricava facilmente x = (15/75) * L = 0,2 * L = 80
D =
0,8 * MAC = 80% della MAC
2) Sa
= 90, Sc = 10, L = 400, MAC = 100,
90*D
= (L – D) *10 D = 0,1 * L =
40, cioè D = 40% della MAC = 0,4 * MAC
Notare
che, a parità degli altri fattori, aumentando solo Sc (oppure L) aumenta D e
quindi aumenta la posizione del PN sulla MAC. Esempio nel caso 1) per Sc = 20
diviene D = 100 (oppure per L = 500 diviene D = 100).
Aumentando
solo Sa (oppure MAC) diminuisce D, senza mai azzerarsi, e quindi il PN avanza
sulla MAC, senza mai portarsi sotto al 25% dal bordo d’entrata.
Avevo
già trattato parte dell’argomento formule nell’articolo FUOCHI = CENTRO AERODINAMICO E
PUNTO NEUTRO in relazione ai centri di pressione ed al baricentro, adesso dettaglierò alcune formule
utili per la stabilità longitudinale.
Prima formula, da me ora detta di Geistware (forse non appropriatamente)
D = L * (Stab
area/(Wing area + Stab area))
PN,
lunghezza a partire dal bordo di entrata della MAC = 0,25 * MAC + (D/MAC) *
MAC.
Nelle sole % della MAC, PN% = 25% + D%
Questa
formula di D, proposta da Geistware nel forum del sito RC Universe, è errata, in quanto
comporta una posizione del PN troppo arretrata, rispetto al senso di marcia, mentre la formula del PN sarebbe
esatta qualora D fosse valutato esattamente.
Esempio,
per il caso bilanciato 1), risulterebbe D = 400 * (15/ (60+15)) = 80
Mentre
per il caso 2) risulterebbe D = 400 * (10/ (90+10)) = 40.
Entrambi
questi casi sono errati, ma coincidenti ai risultati del bilanciamento
grossolano delle superfici. Si può facilmente dimostrare che la formula di Geistware è derivata proprio dallo stesso grossolano ed
errato bilanciamento (e viceversa).
Sa *
D = (L-D) * Sc
Sa *
D = Sc * L – Sc * D
(Sa +
Sc) * D = Sc * L
D =
Sc*L / (Sa + Sc)
Passaggio mentale per collegare D a K tramite Cc.
Sappiamo
che K può variare da circa 0,3 a 1,5, mediamente < 1, normalmente K =
0,6~0,9, fornendo aeromodelli eccessivamente stabili > 1 e scarsamente
stabili < 0,5.
Considerando
valido K = 1 potrebbe essere (Area stabilizzatore*L) = (Area ala*MAC ala), ma
in realtà la stabilità varia secondo il “downwash”
dell’ala e quindi secondo il suo allungamento, oltre che secondo i profili
ala/stabilizzatore, i loro diversi numeri di Reynolds e secondo il diedro
longitudinale aerodinamico.
Ciò che
segue è il punto più difficile da comprendere di tutta questa trattazione,
cercherò di spiegarlo senza matematica, spero senza indurvi in errore.
Con K =
1 la portanza di un volume di coda equilibrerebbe staticamente quella di un
volume sopra l’ala, in assenza di variazioni di momenti dinamici rispetto al
PN, essendoci forze aerodinamiche portanti supposte senza diverse resistenze e
nelle stesse condizioni di flusso, cosa che sappiamo che in realtà non succede,
perché l’ala è più efficace del timone ed il timone di coda è soggetto al “downwash” dell’ala.
Il punto neutro PN
si troverebbe comunque dietro l’AC dell’ala, distanziato nella lunghezza D.
Variando K varierebbe anche D, anzi D risulterebbe funzione di K,
oltre che in dipendenza incognita anche di altri fattori indipendenti da K.
Possiamo porre D =
K * Cc = Sc*L*Cc/ (Sa* MAC).
Ho raggruppato
tutti gli altri fattori in un coefficiente
correttivo Cc.
D può essere visto come semplice prodotto di fattori.
Posto di conoscere,
o supporre valido, Cc * MAC dai successivi metodi, si potrebbe utilizzare
direttamente D in % =
Sc*L*Cc/ Sa.
Ovviamente PN% = 25% + D% perché la
posizione del PN può venir misurata come percentuale della MAC, soprattutto in
funzione dei fattori determinanti D%.
Importante. A parità di Cc, il PN viene spostato da un diverso K nel senso di
marcia lungo la MAC, indietro per K maggiore, oppure avanti per K minore,
tuttavia questo spostamento del PN, anche a pari K, è determinato soprattutto
dal coefficiente Cc.
Metodi scientifici per la determinazione di Cc.
Il calcolo del
punto neutro dovrebbe venir affrontato a rigore in modi non elementari.
La teoria
universitaria conduce per analisi matematica alla seguente formula del PN, per
la quale ad esempio ho raccolto anche le considerazioni presenti nelle tesi di Giuseppe Di Matteo, Marco Giarrizzo,
calcolo PN per un aliante ASH 31, colà vedere alla pag. 43 e 44, per i fattori
dello stesso aliante.
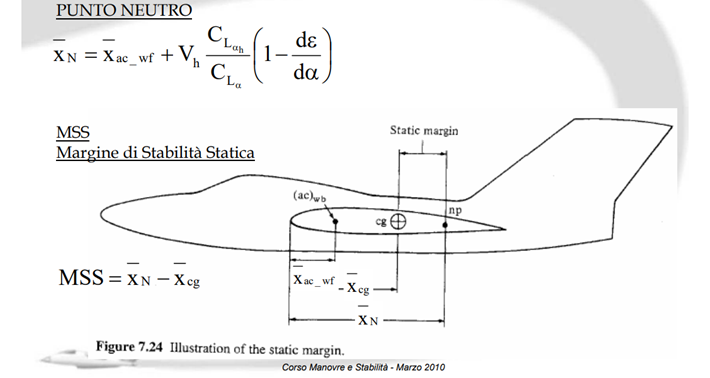
Ecco un’immagine
dalle lezioni di Manovre e stabilità del Prof. Nicolosi.
Vh = rapporto
volumetrico di coda
CLαh =
Coefficiente angolare portanza incidenza coda orizzontale
CLα =
Coefficiente angolare portanza incidenza velivolo completo
dε/dα = derivata dell’angolo di downwash rispetto all’incidenza
Nella pratica aeromodellistica
le stesse considerazioni possono generare metodi più o meno semplificati, come
segue.
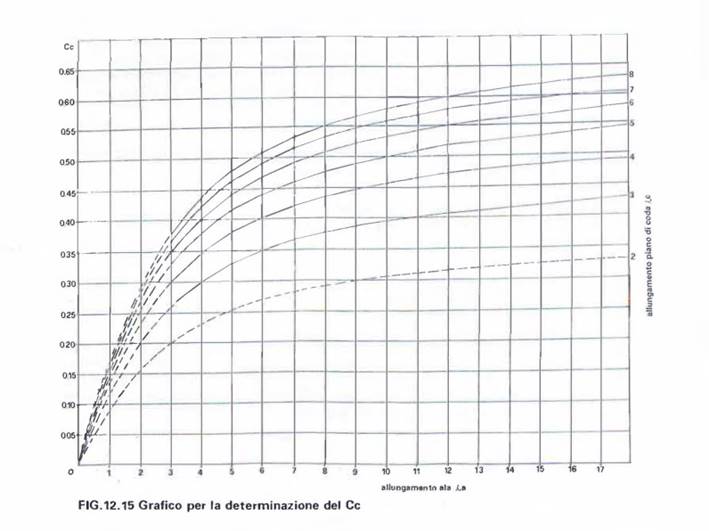
Metodo grafico detto di Cole e Beuermann. Il
metodo compariva già nel magnifico libro di Loris Kanneworff,
1992, Progettiamo gli aeromodelli, pag. 202, da cui riporto il seguente
stralcio ed il grafico FIG. 12.15.
“…se prendiamo ora il fattore (ac/aa)*[1- (dε/dαa)]
e lo chiamiamo Cc , avremo quel famoso coefficiente presentato in forma
di grafico da Beuermann, Cole ed altri studiosi, che
serve a correggere il valore geometrico K del rapporto volumetrico di coda, ai
fini della determinazione del punto neutro…”
Senza
entrare nel merito preciso dei significati e della derivata (dε/dαa), significati determinati dal “downwash” dell’ala che investe lo stabilizzatore dei
modelli convenzionali, supponendo il gradiente di portanza ala vicino al
gradiente di portanza del velivolo completo, essendo:
ε =
angolo di svio, αa = angolo di incidenza dell’ala,
aa =
gradiente di portanza ala, λa = allungamento ala,
ac = gradiente di portanza piano di
coda orizzontale, λc = allungamento
stabilizzatore,
Cc = coefficiente
correttivo per D in % della MAC, dal grafico è
abbastanza facile trovare D e PN nelle seguenti formule, sempre in percentuali
MAC:
D = K * Cc
PN = 0,25 MAC + D
Credo
che questo metodo grafico sia stato seguito perlopiù fino all’avvento dei
calcolatori editabili su PC.
I quali
calcolatori perlopiù predicano bene, ma razzolano male, essendo indicati validi
in generale, cosa che non deve essere, perché ogni aeromodello è diverso. In
tali calcolatori ci si riferisce a formule teoricamente valide, ma in pratica
utilizzate con parametri universali costanti, che non possono essere sempre adatti
nello specifico. Ciò non ostante i risultati sono di solito accettabili, con
buona approssimazione, al punto che qualcuno preferisce addirittura ignorare il
calcolo on line, forse addirittura ignorare ogni riferimento scientifico, ed
impiegare solo la seguente formula
banale, generalizzata in percentuali della MAC, tramite un parametro imposto a
priori, cioè perlopiù viene posto Cc = 0,4 (oppure un diverso valore derivato dall’esperienza
personale, essendo i valori dei Cc reali diversi per alianti, moto-modelli,
trainer, acrobatici etc.).
PN % = 25 + 40 K
2 sistemi di calcolo proposti nei calcolatori on line editabili.
Sistema teorico, ricollegabile ai suddetti metodi
scientifici e grafico, ma realizzato in file editabili di calcolo on line,
sistema da qualcuno chiamato metodo di Martin Simons,
da altri formula di Raymer o formula di Roskam (dai
sacri testi dei suddetti professori), sistema ad esempio ben proposto dal sito RC AeroBase, nell’articolo The Winning Formula, nel quale in inglese potete leggere una dettagliata
disanima copiata dal sito Radio Modeller, ove i
passaggi teorici sono spiegati praticamente per filo e per segno.
Il
suddetto sistema di Simons appare utilizzato nei
calcolatori on line editabili proposti da:
· eCalc
·
Aircraft
Super Calculator – Holdfast Model Aero Club
·
The Skyhopper Ultralight_ Super Calc
Lo
stesso sistema appare utilizzabile anche nel sito RC AeroBase,
però tramite file Excel.
Io qui
riassumo tale sistema nella formula teorica, espressa in termini da moltiplicare tutti
per la MAC alare onde raggiungere la lunghezza della
posizione NP, cioè, a partire dal bordo di entrata dell’ala, posizione NP = 0,25 + Se * K * (ac/aa) * [1- (dE/dx)]
Simbologia,
analoga alle precedenti simbologie scientifiche e del grafico, precisando:
Se =
efficienza stabilizzatore, variabile da 0,6 a 0,9, efficienza considerata
poi ad esempio 0,7
(è un ulteriore coefficiente correttivo del prodotto al
secondo addendo dell’equazione; tale coefficiente non compare nella teoria
scientifica di base, forse è introdotto per tener conto che lo stabilizzatore
rende meno dell’ala come rapporto di planata, cioè portanza/resistenza stab., rapportato all’efficienza dell’ala, o forse è un inutile
preziosismo…)
dE/dx = dε/dαa
AR = aspect ratio = allungamento = λ
a = slope of (wing or tail) aerofoil lift curve =
pendenza della curva di portanza del profilo (per ala = aa, oppure per coda = ac).
ac/aa = CLαh/CLα. Invero qui si
confonde la pendenza della curva di portanza dell’ala
con quella del velivolo completo, in quanto portanze considerate simili, salvo
un imponente effetto fusoliera, pure trascurato. Comunque in realtà le
pendenze delle curve delle portanze sono solitamente poco note, pertanto nei
calcolatori on line credo vengano stimate approssimate, conoscendo gli AR, in
corrispondenza di valori spero ben tabulati …………..
Per ARa = 6 consegue aa = 0,077, mentre per ARc
= 4 consegue ac= 0,069.
ac/aa = 0,069/0,077 = 0,9 = valore
considerato poi nella praticizzazione del calcolo.
dE/dx = rozzamente = 35 *aa/ARa = 35 *0,077/6 = 0,45 cioè
dE/dx = 0,45 per i monoplani di
allungamento alare 6, quindi [1- (dE/dx)] = 0,55.
NP =
0,25 + 0,7 * K * 0,9 * 0,55 = 0,25 + 0,35 K
Per K
= 0,6 il punto neutro sarà a quasi metà MAC.
Nell’esempio
proposto da Radio Modeller si arriva ad un risultato
praticamente identico alla formula banale già esposta in precedenza, il che potrebbe dimostrare che i siffatti calcolatori on
line editabili servono a poco, in casi diversi da una soluzione standardizzata,
salvo conoscere gli effettivi singoli valori determinanti il Cc globale nei
casi di aeromodelli non standard, inoltre nella supposizione che tali
calcolatori consentano di precisare singolarmente tutti i valori nel loro
software, cosa che non mi pare in generale.
Sistema pratico basato sulla radice quarta
dell’allungamento alare = ARa = ARw
Si
tratta apparentemente di un sistema più semplice del precedente.
Esso
viene proposto come calcolatore on line editabile da:
·
RC Planes (Aircraft Center of Gravity
Calculator)
·
Amman Valley Radio Control Club (Aircraft Super Calculator 6.1)
·
AVRCC - C of G Calculator
L’equazione
di base è la seguente, già proposta nel mio sito alla pagina FUOCHI =
CENTRO AERODINAMICO E PUNTO NEUTRO in relazione ai centri di pressione ed al
baricentro.
NP =
0.25 + (0.25 * sqr(sqr(ARw)) * Vbar
Avevo anche tentato di spiegarne la
logica nel Forum Barone Rosso, tramite un messaggio che nel seguito ho qui integrato.
Il risultato della posizione di NP, puramente
orientativo, è molto vicino alla realtà, ma il metodo credo che sia arbitrario.
Da considerazioni sperimentali si sa
che quasi tutti gli aerei convenzionali a coda posteriore hanno l'NP variabile
dal 35 al 65% circa della MAC, quindi poniamo 50% come valore medio indicativo
della base di calcolo.
Poniamo quindi che 50% = (0,25 + 0,25) MAC. Il
primo 0,25 MAC è chiaramente la posizione dell'AC (Aerodynamic
Center) dell'ala, che sappiamo essere in posizione quasi costante.
Il secondo addendo può variare incognitamente
per ogni aereo specifico, da richiedere una correzione oculata, che è stata
resa dipendente da Vbar e dall'allungamento alare.
Calcolando la radice quarta dell'allungamento
alare come un coefficiente correttivo di Vbar, matematicamente, aumentando l’allungamento alare, aumenta
la sua radice quarta, quindi aumenta il prodotto [(0.25 * sqr(sqr(ARw)) * Vbar],
quindi, a parità di Vbar, con l'aumentare dell'allungamento alare, l'NP
dovrebbe spostarsi un poco indietro sulla MAC, mentre, diminuendo l'allungamento alare, l'NP
dovrebbe spostarsi un poco avanti sulla MAC, vista nel
senso di marcia.
Infatti, se
aumenta l’allungamento alare dovrebbe diminuire il downwash
verso la coda, quindi lo stabilizzatore aumenta di
efficienza, soprattutto portanza, e nell’equilibrio, con la coda più portante, l’NP dovrebbe
spostarsi indietro. Anche il CG per l’equilibrio si sposta indietro, a
pari stabilità con pari margine statico.
E’ altrettanto vero che, siccome anche l’ala è
più efficiente con l’allungamento più alto, a seguito di ciò, per l’equilibrio,
se la portanza alare aumentasse, l’NP dovrebbe spostarsi un poco avanti nel
senso di marcia, tuttavia ciò credo succeda poco, perché l’efficienza dell’ala
migliora soprattutto per la diminuzione della resistenza indotta, senza che ci
sia un sostanziale aumento della portanza, a superficie alare costante.
In realtà con diverso ARw anche
la portanza alare cambierebbe un pochino, ma qui non considero le variazioni di
portanza alare. Quando l’ala è parimenti
portante il PN non si sposta avanti.
Il minor effetto downwash
dell’ala anteriore sullo stabilizzatore posteriore, tramite un maggior
allungamento dell’ala a parità di superficie alare, favorisce pertanto una
stabilità maggiore.
Se, ponendo allungamento = 1, si fosse scelto per il secondo addendo della formula soltanto
0,25*Vbar, essendo Vbar un coefficiente
solitamente variabile tra 0,3 e 0,9, ad esempio in media Vbar=0,6,
sarebbe risultato un valore di NP non sempre rientrante nei sopraddetti valori
sperimentali, oscillante sulla media NP = 0,4 MAC con valori estremi troppo
bassi, cioè circa posizioni di NP nel campo percentuale dal 32,5% al 47,5%
della MAC.
(Sarebbe stato come scrivere NP% = 25 + 25 K)
Ma se fosse stato Ara = 20 senza la radice
quarta, sarebbe risultato NP% = 25 + 500 K, cioè sarebbe risultata una
posizione di NP eccessivamente arretrata, quasi in corrispondenza dello
stabilizzatore e dunque una posizione sperimentalmente decisamente errata.
Inoltre anche a logica l’NP potrebbe
arretrare, ma non indietro oltre lo stabilizzatore ……
Invece introducendo la radice quarta risulta
NP% = 25 + 25*2,12 K = 25 + 53 K.
Allora ecco la genialata del calcolatore, dove
il secondo addendo è stato appunto posto in funzione anche della radice quarta
dell'allungamento alare, radice che, per allungamenti alari variabili da 1 ad
esempio 20, siccome sqr(sqr(ARw)) varia circa da 1 a 2,11, tale ulteriore coefficiente
è usabile come fattore moltiplicativo e correttivo del prodotto (0.25 * sqr(sqr(ARw)),
prodotto che quindi varia da 0,25 a massimo 0,5286.
(Se nella formula con la radice quarta si fosse
posto sempre Vbar=1, le posizioni estreme di NP sulla
MAC dovute al solo allungamento sarebbero risultate troppo arretrate rispetto
al campo sperimentale dal 35 al 65%, cioè ad
esempio per ARa =1 sarebbe risultato NP% = 25 + 25 =
50 %, oppure per Ara = 20 sarebbe risultato NP% = 25 + 53 = 78%.
Eventuali posizioni oltre il 78% escono dal
campo indicato come sperimentale, ma sono tuttavia accettabili fino ad un
limite da individuare. Nei modelli Old timer tali
posizioni dell’NP sono state pienamente accettate anche ben dietro al bordo di
uscita della MAC).
Ecco che il calcolatore, moltiplicando tra
loro tutti i membri del secondo addendo, ha introdotto quindi, con la radice quarta di ARa >1, un aumento rispetto al campo del solo Vbar (campo che era, per V bar tra 0,3 a 0,9, con NP
variabile dal 32,5% al 47,5% della MAC), ma ha anche introdotto una diminuzione rispetto al
campo di NP dovuto al solo allungamento alare, limitando in conclusione il
valore del secondo addendo entro limiti precisi, ai quali occorrerà aggiungere
0,25 = 25% del primo addendo, per trovare la posizione di NP.
Penso che la radice quarta dell’allungamento alare,
riducendo moltissimo il prodotto del secondo addendo della formula, sia stato
un buon trucco per limitare l’eccessiva importanza di tale addendo con ARw senza radice, e quindi per far avanzare il PN in una
posizione accettabile.
Mentre per Vbar = 1 il campo è, per ARa tra 1 e 20, con NP variabile
dal 50 al 78% della MAC, nei valori per Vbar < 1 per esempio:
- considerando Vbar = O,3 il campo della posizione di
NP varia (da 0,075 a 0,158) + 0,25 = varia da 0,325 fino a 0,408, cioè dal
32,5% fino al 40,8% della MAC.
- considerando Vbar
= 0,6 il campo della posizione di NP varia (da 0,15 a 0,317) + 0,25 = varia da
0,4 fino a 0,567 * MAC, secondo gli allungamenti variabili da 1 a 20.
- considerando Vbar
= 0,9 il campo della posizione di NP varia (da 0,225 a 0,475) + 0,25 = varia da
0,475 fino a 0,725, cioè dal 47,5% fino al 72,5% della MAC.
In conclusione tutto il campo delle possibili
posizioni di NP lungo la MAC è risultato compreso dal 32,5% fino al 72,5%,
posizioni percentuali che sono da ritenersi adeguate a coprire tutto il campo
degli esperimenti, come volevasi dimostrare.
La posizione media di NP per K = 0,3 ~ 0,9
risulterebbe al 52,5 % della MAC, praticamente vicina al 50% dell'ipotesi fatta
all'inizio (pur con un errore del 4,76%), ma per K = 0,6 il punto neutro
risulterebbe al 48,35% della MAC (con errore 3,3%). Con ARa
= 10 risulterebbe NP = 51,67%.
Per avere NP = 50% occorrerebbe sqr(sqr(ARw)) * Vbar
= 1, risolvendo la quale, ad esempio per K = 0,6 si ottiene sqr(sqr(ARw)) = 1,66666, cioè quasi il numero
aureo = 1,618033988
= Φ.
Per quanto concerne Φ
vedere avanti il capitolo Aerodinamica mirabolante (*), per il quale ho già
pubblicato, ancora nel Forum del Barone Rosso,
un “trend” dal titolo Calcolare il punto neutro.
Tuttavia l’NP al 50% si può ottenere dalla stessa equazione
anche con fattori ben diversi, cioè con diversi K e quindi diversi ARw, senza apparente necessità di tirare in ballo il
Φ.
Esempio per NP =50%, oltre che per K = 0,6 con ARw =7,716, potrebbe
valere anche K = 0,7 con ARw = 4,164, essendo sqr(sqr(ARw))
= 1,4285.
A mio avviso tuttavia Φ può essere sempre collegato al
volo degli uccelli, ed anche a quello dei velivoli che li copiano, tramite diversi
indici di radici od esponenti n in base Φ, come si vedrà, studiando il
volo di uccelli diversi dalle aquile; nella fattispecie dell’ultimo esempio (ARw ~ 4) si potrebbero considerare i piccioni (Columbiformes),
invece di considerare gli Aquilinae, o più
estesamente gli Accipitriformes (aquile, avvoltoi,
condor etc.) e, quando simili per allungamenti alari, alcuni Anatidi (anatre e
cigni), nonché le cicogne.
Invece per
Vbar > 1 il punto neutro può andare indietro
oltre il 78% (come negli aeromodelli Old timer).
Esempio per Vbar =
1,5 risulterebbe NP variabile dal 62,5% fino al104,3% della MAC, cioè NP
potrebbe andare immediatamente dietro al bordo di uscita della MAC per ARa = 20.
Osservare che il prodotto (0.25 * sqr(sqr(ARw)) è sempre minore di 1 e
i Vbar proposti inizialmente erano minori di 1,
dunque li prodotto [(0.25 * sqr(sqr(ARw)) * Vbar] = D era sempre
frazionario, minore di 1.
Il prodotto sqr(sqr(ARw) * Vbar può
essere invece l’unico prodotto maggiore di 1, mentre 0,25*Vbar
è sempre <1 per Vbar <4, cioè in pratica
sempre.
Siccome sempre Vbar < 2 e siccome ARa al massimo potrebbe divenire perfino = 40,
[(0.25 * sqr(sqr(ARw)) * Vbar]
= D al massimo diviene 1,257 = 125,7% = D% = valore ben accettabile per il massimo
arretramento possibile del PN al 150,7% MAC.
(*) Aerodinamica mirabolante.
Svelato il segreto delle aquile?
Ricopio nel
seguente riquadro le parti salienti già proposte nel Forum
Barone Rosso, correggendo la nota formula dell’NP, contenente la
radice quarta di ARw, tramite l’aggiunta, nel
prodotto nel secondo addendo, di un fattore correttivo contenente il valore del
diedro longitudinale geometrico DL, espresso in gradi sessagesimali, ma intesi adimensionalmente, nel seguente modo.
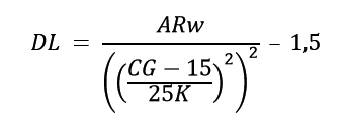
Precisamente ho moltiplicato il secondo addendo per 
(1/ (DL +1,5). Ricordo che la radice quarta di un prodotto
uguaglia il prodotto delle radici quarte, pertanto talora scriverò la nuova
identica formula in diverse forme matematiche, allo scopo di facilitarne il
calcolo, ma si tratterà sempre della stessa mia formula.
Il coefficiente
1,5 è stato messo al denominatore di X = 1/(DL + 1,5)
per non mandare il rapporto 1/DL all’infinito, nel caso DL = 0.
Se non avessi messo la radice
quarta di X, moltiplicando solo 1/(DL +1,5)* sqr(sqr(ARw))*
K, il
prodotto avrebbe dato valori troppo bassi al secondo addendo dell’equazione
dell’NP.
Avrei potuto
usare in alternativa solo la radice semplice, cioè fare X = 
, tuttavia si sarebbe ottenuto un
risultato ancora basso, allora ho scelto di mettere l’incognita X sotto radice quarta.
Esempio per DL = 2,5 X = 0,25 sqrX = 0,5 sqrsqrX = 0,707
= accettabile e accettato.
|
Osservare che non esiste un unico CG valido, ma il CG può essere
ottimizzato in una gamma di posizioni dipendenti dal diedro longitudinale.
Riassumendo, nella maggioranza dei casi si può trovare la MAC
tramite il seguente metodo grafico, indi
applicare la formula proiettandone i
risultati percentuali della MAC sull’asse longitudinale in fusoliera
dell’intero velivolo. Nota. Cambiare il DL è quasi come passare da una situazione a
comandi bloccati ad una diversa situazione a comandi liberi e bloccare il
comando libero nella nuova situazione. Cioè cambiare il DL è quasi
come spostare l’equilibratore rispetto allo stabilizzatore orizzontale di
coda. Però non è esattamente la stessa cosa, come discusso, a partire da pag.
5 in poi, fino a pag. 11, al sito:
|
Numero
aureo = 1,618033988 = Φ = phi,
lettera maiuscola nell’alfabeto greco (minuscolo ϕ).
Il numero aureo si ottiene considerando due
numeri, a & b, con a > b, tali che il rapporto tra la somma dei due
numeri (a+b) ed il numero maggiore (a) sia uguale al
rapporto (a/b) tra il numero maggiore e quello minore.
Per
l'equilibrio di un volatile poniamo che sia sempre NP ~ 50% MAC, perché per lo
più “in medio stat virtus”,
ma non è sempre vero.
Nella
formula dell'NP = 25 + 25 * (sqr(sqrARw))
* K, senza conteggiare il DL, se
fosse sqr(sqr(ARw)) = ϕ, risulterebbe
ARw = ϕ^4 = 6,854, che potrebbe essere l'allungamento alare di
alcuni ottimi volatili, in particolare le aquile.
Infatti, se indaghiamo l’aquila delle steppe (Aquila nipalensis Hodgson, 1861), dalle tesi di laurea Ing. Bivona ( https://areeweb.polito.it/fluidlab/t...na_BA_2014.pdf ) – Lonoce (
https://areeweb.polito.it/fluidlab/t...ce_BA_2014.pdf ), apprendiamo che l'apertura
alare = 200 cm e la corda media = 30 cm (che possiamo assimilare alla lunghezza
MAC).
Dunque tale aquila avrebbe allungamento =
6,666 (con
superficie alare Sa = circa 0,6 m^2 perché l’ allungamento è b^2/Sa,
ove b^2= quadrato dell’apertura alare. Quindi
4/Sa = 6,66 dunque Sa = 0,6 m^2). L'allungamento alare delle
aquile è dunque prossimo a 6,854.
Pur essendo quasi impossibile sapere dalla
letteratura i rapporti volumetrici di coda (K) degli uccelli, c'è però un
collegamento aerodinamico tramite la stessa formula, ponendo NP% = 50.
50 = 25 + 25 * 1,618033 *
K donde risulta K = 0,618033.
Tale
valore di K potrebbe quindi essere proprio il K delle aquile, e pertanto lo intenderei adatto alla miglior
stabilità di volo di velivoli in analoghe condizioni di volo delle aquile.
Notare che 1/1,618 = 1,618 - 1 = 0,618. Dunque, avendone già posto in
relazione l'allungamento alare, anche il presunto K delle aquile si può porre
in stretta relazione al numero aureo, qualora la posizione di NP fosse
costantemente = 50% MAC.
Apro qui una digressione sulla magia, senza cadere nell’occultismo.
In matematica 6 è considerato il
primo numero
perfetto. In religione invece è “imperfetto”.
Esiste in natura
un’impressionante legame con il numero 6 (ritrovabile nel così detto numero del
diavolo o della
bestia = 666 o 616, in opposizione al numero
teologicamente, ma non matematicamente, perfetto 7). Notare che il reciproco 1/6,16227 =
0,16227 è il sesto dei reciproci particolari, dei quali Φ = 1,618…è invece
il primo reciproco particolare.
Diciamo che il 6 si ritrova
in tutti i seguenti numeri, posto prima o dopo la virgola dei decimali:
1,618034 – 0,618034 - 6,854
~ 6,66 – 0,6 – 6,16277 – 1,6666, numeri che possiamo vedere collegabili all’ARw ed al K degli aquilini, a condizione che NP = 50%.
Lasciando perdere la bestia
ed i misteri dell’occultismo, ho inteso il valore (Φ – 1) come media
ideale per il K da utilizzare per la miglior stabilità degli aquilini, ma non
per gli altri volatili.
Infatti K ~
0,618034 potrebbe essere invero 0,6 oppure 0,7 e gli aquilini volerebbero lo
stesso; anche altri volatili volerebbero con simili K, ma con allungamenti ben
diversi.
Notare
che era NP = 50% anche con K =0,6 e ARw = 7,716,
essendo sqr(sqr(ARw)) = 1,6666, ma potrebbe valere ad esempio anche K = 0,7
con ARw = 4,164, essendo sqr(sqr(ARw)) = 1,4285, senza
necessità di tirare in ballo il Φ. Tuttavia si vedrà in Conclusione che per altri uccelli il
Φ può entrare ancora in ballo, ma in diverse forme esponenziali o
radicali.
Rivediamo tutto il discorso aggiungendo, nella formula del punto
neutro, la radice quarta di 1/(DL+1,5), sempre con NP supposto al 50 % MAC.
Siccome un minimo diedro longitudinale geometrico DL negativo è possibile, il
risultato sarebbe guarda caso identico con DL = - 0,5 (gradi sessagesimali
idealmente adimensionalizzati).
Pertanto avremmo NP = 50% ponendo K = 0,618 con ARw = 6,854 e DL = - 0,5.
Sempre con ARw = 6,854, se invece fosse DL = 0, dalla mia formula invece risulterebbe sorprendentemente K = 0,6839 ~ ARw/10 = 0,6854 = ϕ^4/10.
Cioè il rapporto volumetrico di coda
(soltanto) delle aquile, allorquando il DL fosse nullo, uguaglierebbe circa
1/10 del loro allungamento alare derivato dal numero aureo.
Esisterebbe dunque una relazione aurea tra K, ARw e DL delle aquile, basata circa sulla cifra tonda 10,
con DL ~ 0. La cifra tonda 10 varrebbe
però solo nel caso delle aquile, infatti per altri volatili il rapporto ARw/K mi appare ben diverso da 10, in assenza di relazioni
al ϕ.
Mentre nelle aquile (e negli uccelli), mutando
la superficie e l’inclinazione della coda, sarebbe possibile mantenere l’NP al
50% cambiando K in seguito ad un cambiamento del DL, negli aeromodelli ed
aerei, una volta costruiti, K e ARw non possono
variare, al mutare del DL.
Ad esempio, con gli stessi indicatori
dell'aquila, prefissando (sia nell'aquila che) in un modello K = 0,6854 e ARw = 6,854, cambiando soltanto il DL (o la posizione
dell’equilibratore), cambierà la posizione del punto neutro (e quindi la posizione di
equilibrio del CG, volendo un pari margine statico),
come nel seguito risulterebbe dalla mia
formula.
Per DL < - 1,5 matematicamente risulterebbe
NP all'infinito dietro la MAC, ma credo che tale DL non debba mai essere
utilizzato (1,5 è il coefficiente dubbio della mia formula, per la validità
della quale occorre imporre sempre DL>> - 1,5 )
Per
DL = - 1 risulta NP = 25 + 25 * 1,1090 * sqr(sqr(1/(DL + 1,5))) = 57,970%
Per DL = - 0,5 risulta NP = 52,725%
Per DL = 0 risulta NP = 50,052 %
Per DL = 0,5 risulta NP = 48,313%
Per DL = 1 risulta NP = 47,048%
Per DL = 2 risulta NP = 45,270%
Per DL = 4 risulta NP = 43,104%
Per DL = 8 risulta NP = 40,792% tuttavia potete
in tutti questi casi tranquillamente trascurare tutti i decimali, perché i
risultati % dell'NP, e del conseguente CG % MAC, sono solo indicativi, da
verificare poi sperimentalmente in volo.
Cambiando le posizioni del punto neutro, che
ricordo sono tutte in percentuali della corda aerodinamica media (MAC) a
partire dal bordo di entrata ala, il margine statico (NP - CG) cambierà
rispetto alla posizione prefissata del CG sul modello. Se si vuole mantenere lo stesso margine statico
(solitamente pari al 10% MAC a partire dall'NP in avanti secondo la direzione
di volo), occorre mutare la posizione del CG.
Viceversa, se l’NP restasse bloccato
al 50% occorrerebbe cambiare K in seguito ad un cambiamento del DL nella mia
formula. Ad esempio solo per gli aquilini sempre con ARw
= 6,854
Per DL = - 1 risulterebbe 50 = 25 + 25 * 1,618
* sqr(sqr(1/(DL + 1,5))) *
K
1 = 1,618 * sqr(sqr(1/0,5)) * K 0,618 = 1,1892 * K K
= 0, 5196
Per DL = - 0,5 risulterebbe K = 0,618
Per DL = 0
risulterebbe K
= 0,6839 ~ ARw/10
Se il DL fosse + 0,5, essendo sqr(sqr(1/(DL+1,5))) = 0,840, la
formula darebbe K = 1/1,359 = 0,735.
Se fosse DL = 1 sarebbe sqr(sqr(1/(DL+1,5))) = 0,7952, pertanto per NP = 50 = 25 + 25 *
K * 0, 7952 * 1,6180 risulterebbe K =
0,777
Per DL =2 risulterebbe K = 0,845 …….etc.etc. fin
massimo per DL = 8 K = 1,085
Ho poi pensato che, al
posto del coefficiente 1,5, inizialmente scelto empiricamente, si potrebbe
usare forse
più esattamente Φ, ma ciò risulta senza un sensibile
vantaggio nel calcolo pratico del CG. Rimane comunque sconcertante come la
casualità quasi azzeccata della mia scelta iniziale di 1,5 approssimi
grossolanamente il numero aureo.
Per esempio ancora restando nel campo degli
aquilini, per DL = 0 e NP = 50, con ARw = 6,854, ma
mettendo sotto radice quarta 1/(DL + ϕ),
risulta K = 0,697
In paragone ai risultati di NP% trovati
precedentemente con K = 0,6854, prefissando
adesso sempre K = 0,697 e ARw = 6,854 (con
rapporto ARw/K = 9.8335 invece di 10), succede che:
Per DL < - 1,6180339 risulterebbe NP IMPOSSIBILE, ma
tale DL non deve mai essere utilizzato (per la validità della mia formula
occorre imporre sempre DL>> - ϕ)
Per DL = - 1 risulta NP = 25 + 25 * 1,12776 *
sqr(sqr(1/(DL + 1,618))) = 25 + 25 * 1,12776 * 1,12784 = 56,798
%
Per DL = - 0,618 risulta NP = 53,194 %
Per DL = - 0,5 risulta NP = 52,418 %
Per DL = 0 risulta NP = 49,998 %
Per DL = 0,5 risulta NP = 48,370 %
Per DL = 1 risulta NP = 47,164 %
Per DL = 2 risulta NP = 45,442 %
Per DL = 4 risulta NP = 43,313 %
Per DL = 8 risulta NP = 41 %.
Se invece si prefissasse ancora K = 0,6854, usando la
formula NP=25+25K*1,618 * sqr(sqr(1/(DL + 1,618))), per mantenere NP = 50% occorrerebbe DL =
- 0,1055.
Se infine si prefissasse K = 0,618 per mantenere NP = 50%
occorrerebbe DL = - 0,618.
Conclusione.
Allo scopo di studiare con minori complicazioni i volatili
diversi dagli aquilini, per il momento non considererò il DL nella formula dell’NP.
Il K degli aquilini ho scritto che potrebbe essere circa =
allungamento/10 = 0,6854 = Φ^4 (ma potrebbe essere anche ~ 0,7, ponendo Φ al posto del coeff. 1,5, ed anche potrebbe essere >> 0,7 se
l’aquila volesse mantenere l’NP al 50% aumentando il DL o/e diminuendo ARw); comunque, credo che, anche secondo le condizioni di
volo, planato o battuto o picchiato, il K degli aquilini potrebbe variare da ~ 0,6 o 0,618 fino (a 0,6839,
o a 0,6854,
o a 0,697, valori trovati in precedenza, o anche fino) a >> 0,7. Tra tutti questi valori ritengo “standard” K = 0,618 per quanto già scritto per l’aquila delle
steppe, sebbene per la precisione dovrebbe essere invece ̴ 1/1,6 = 0,625.
Nell’ampio spettro dei valori di K, credo che esista anche
per altri volatili, una corrispondenza a Φ.
E' fuor di dubbio che alcuni uccelli volino meglio di
altri, diciamo che possiamo classificarli in successione per efficienza aerodinamica, non volendo assolutamente
classificarli per velocità.
E' altrettanto fuor di dubbio che l'efficienza aumenti con
l'allungamento alare ARw.
La media degli allungamenti alari degli uccelli volatori è
tra 5 e 7, ma ARw può variare da circa 3 (volo balistico)
fino a 18,7 (che è il massimo conosciuto, quello dell’albatros, per volo a vela
oceanico = dynamic soaring).
Gli uccelli diversi dalle aquile, con diversi allungamenti,
possono corrispondere a diverse potenze del numero aureo, con esponente n, che
in un primo tempo avevo pensato essere solo un numero naturale, ma n può essere anche decimale!
Infatti esistono
uccelli per l’allungamento alare dei quali, come esponente n di Φ, si possono utilizzare numeri
decimali, in successione continua. Ciò complica il calcolo di Φ^n,
ma permette di estendere i valori degli allungamenti ARw
a qualsiasi volatile, per esempio utilizzando una calcolatrice on line per le
potenze di esponente n.
Φ potrebbe influire in 3 modalità, partendo dalla seguente tabella,
ove ho dato per valida la formula NP = 25
+ 25 K sqrsqr ARw. Con NP = 50%, risulta K = colonna K. Ecco le 3
modalità:
1) influenza di Φ^n sull’allungamento alare ARw.
La corrispondenza è immediatamente leggibile nella
tabella.
|
Uccelli |
ARw |
Φ^n |
K |
ARw/K |
ARw/0,618 |
NP% |
|
Con ala minima per volare? |
1,618 |
Φ |
0,8866 |
1,8249 |
2,618 |
42,425 |
|
Per volo balistico circa |
2,618 |
Φ^2 |
0,786 |
3,330 |
4,236 |
44,65 |
|
Passeri |
3,33 |
Φ^2,5 |
|
|
5,388 |
|
|
Piccioni (& corvi?) |
4,236 |
Φ^3 |
0,697 |
6,077 |
6,854 |
47,16 |
|
Anatidi & cicogne? |
5,388 |
Φ^3,5 |
|
|
8,718 |
|
|
Aquilini |
6,854 |
Φ^4 |
0,618 |
11,090 |
11,090 |
49,998 |
|
Marini costali (gabbiani) |
11,090 |
Φ^5 |
0,548 |
20,237 |
17,944 |
53,19 |
|
Pelagici (albatros) |
17,944 |
Φ^6 |
0,485 |
36,997 |
29,035 |
56,79 |
Vale inoltre la seguente spataffiata.
Al variare di ARw, per effetto di una supposta costanza
di K = 0,618, passando alla riga
successiva della tabella il rapporto ARw/0,618, soltanto nei casi di n non decimale,
uguaglia l'allungamento della riga successiva, valendo ARw
= 1/ K^n soltanto per K=0,618 con NP = 50% MAC, il
che è come dire che è sempre 0,618 = K = 1/radice n-esima di ARw.
Infatti la radice terza di 4,236 = 1,618 = radice quinta
di 11,09 = radice sesta di 17,944 =1,618. Ho esplicitato
la radice terza, quinta e sesta perché non si possono calcolare con una
calcolatrice elementare, tuttavia il risultato discende da logica matematica.
In realtà di questa spataffiata non ce ne
importerebbe quasi nulla, se non per ciò che potrebbe riguardare l’efficienza
aerodinamica.
2) influenza di Φ^n sull’efficienza
aerodinamica, tramite il rapporto ARw/K, influenza
solo nel caso K = 0,618?
In natura K non mi appare variare molto al modificare
dell'allungamento, mentre varia molto il rapporto ARw/K. Sono sempre rimasto meravigliato della grande
variabilità dei K ritenuti validi per la stabilità, notando però che la media
dei K più validi per la maggioranza degli aerei ben stabili è circa = 0,7,
comunque K è perlopiù < 1.
Fissando K = 0,618 risultano gli NP della colonna NP% ed i rapporti della colonna ARw/0,618.
Orbene l'efficienza
degli uccelli potrebbe essere
collegata al numero aureo dal rapporto ARw/0,618, anzi tale efficienza sembrerebbe
quasi uguagliare (sempre solo) tale
rapporto.
In Wikipedia si cita l’efficienza dell’albatros 22-23, io
ho tabulato ̴ 29, ma in realtà forse ARw
albatros < 17,944, forse ARw ̴ 14. Quindi
l’efficienza dell’albatros potrebbe essere 14/0,618
= 22.65, tuttavia sarebbe meglio considerare Φ^5,5
con K = 0,618. Ricalcolando il tutto, per l’albatros risulterebbe ARw = 14,105 con efficienza 22,82.
Per n decimale risultano valori intermedi che non
corrispondono alla riga successiva della tabella, ma corrispondono a valori
successivi in righe non successive.
Dire che l’efficienza degli uccelli uguaglia ARw/0,618 sarebbe quasi come dire che l’equilibrio nell’NP
al 50% MAC, equilibrio determinato solo realizzando tale rapporto, non dipende
dalle prestazioni dei profili delle ali degli uccelli, profili che determinerebbero
l’efficienza non tramite le loro caratteristiche, ma solo tramite la costante Φ variamente elevata ad n negli ARw
degli uccelli.
Probabilmente si tratta una semplice casualità, perché mi
sembra poco credibile che il rapporto di planata, inteso all’italiana anche
come Cp/Cr, o all’inglese come CL/CD, cioè come
rapporto tra i coefficienti di portanza e resistenza del profilo alare, possa
essere accumunato esclusivamente al rapporto ARw/0,618,
relazionabile soltanto all’ NP = 50% MAC.
Infatti i vari uccelli con K = 0,618 costante
presenterebbero uno spostamento dell’NP dalla posizione 50%, secondo i loro
allungamenti, oppure potrebbero anche nelle varie condizioni di volo mantenere
l’NP al 50% mutando il loro K, ma nessuno sa dove, come e quando gli uccelli
mantengono l’NP nelle varie condizioni di volo e con quale K effettivamente
volino, mantenendo ARw sempre costante (il che è una
falsità, considerando inoltre talora la digitalizzazione delle penne delle
estremità alari).
3) influenza di Φ^n su K
Il rapporto volumetrico di coda (K) appare negli
aeromodelli una variabile indipendente, tramite la quale determinare
l’equilibrio e/o la stabilità, ma in natura, essendoci una relazione col numero
aureo, potrebbe esserci una dipendenza diretta e totale da esso, o da suoi
derivati?
Se vale la formula
NP = 25 +25 K sqrsqr ARw,
solo con NP = 50% ,
essendo ARw = Φn , risulta K = 1/ sqrsqr Φn ove n = esponente di Φ.
Attenzione che facendo le radici quarte di Φn il risultato offre n valori
di K diversi, cioè come quelli della colonna K della tabella, valori K che sarebbe più indicativo
chiamare Kn .
L’equazione aurea basica Kn = 1/ sqrsqr
Φn collega Kn a Φn soltanto per NP =
50% MAC, ma nessuno ci dice che NP è proprio al 50%, a meno che l’esponente n
determini o sia determinato dalla posizione di NP, comunque non lo sapremo mai
esattamente.
In conclusione le aquile forse hanno l’NP al 50%, mentre altri uccelli
forse hanno l’NP spostato, con Kn variabile.
Vale comunque una specie di
effetto di scala: uccelli piccoli, o meglio
con scarsa efficienza, hanno K più elevati, cioè stabilizzatori di superficie
più grande e/o stabilizzatori più lontani dall’ala, con ali meno “aureizzate” nell’allungamento, posto ARw
= Φn
Il risultato della modifica
della formula in NP = 25 +25 K * ARw * (1/ (DL +1,5), con DL positivo porta l'NP
leggermente avanti, nella direzione di volo, rispetto all'uso della formula
originale senza * (1/ (DL +1,5), formula originale usata per lo più nei calcolatori on
line. Se si dà per scontato che la formula originale è valida, si deve
accettare che i valori di NP e K trovati per gli aquilini sono probabilmente
validi, e sono validi anche per la maggioranza dei modelli volanti come le
aquile. Se si ritiene che l’aggiunta del prodotto * (1/ (DL +1,5) sia una miglioria della formula originale, si deve
accettare che con DL positivo l'NP si sposti leggermente avanti, e quindi debba
anche avanzare il CG, anche con NP diverso dal 50% e K variabile nella gamma
usuale.
Tuttavia non si deve
considerare l’avanzamento del CG un ossequio alla massima "modello
picchiato modello salvato", infatti il CG dovrebbe avanzare, con l’NP
sotto il 50%, soltanto allorquando il DL fosse crescente da un valore prossimo
allo 0 in su, fin verso al massimo 6°, o 8° esagerando, nel prodotto * (1/ (DL +1,5), oppure meglio, se si vuole, * (1/ (DL +Φ).
Per me resterà un mistero
il fatto che un aeromodello convenzionale possa volare con K variabile da 0,3
fino a 1,5 circa, cioè in una gamma di valori di
K così troppo estesa, al punto da invalidare la scelta del K migliore, come
valore troppo opinabile, sebbene in campo aeronautico “full size”
la scelta si restringa attorno a K = 0,6 circa.
Update 30.05.2024. Questa pagina viene proposta ad integrazione dell’articolo
FUOCHI = CENTRO AERODINAMICO E PUNTO NEUTRO in relazione ai centri di
pressione ed al baricentro.
Spero di poter chiarire e correggere in futuro alcuni punti
ancora oscuri o errati.
Grazie dell’attenzione, ogni suggerimento e consiglio sarà
gradito.
Flavio Mattavelli matta.a@tiscali.it
Home page: http://www.pseudospecie.it
Indice generale: http://www.pseudospecie.it/Indice.htm